量子比特与量子门¶

1. 量子比特¶

量子术语与线性代数术语对照¶

量子力学术语	线性代数术语
态矢量 (State Vector)	向量 (Vector)
本征态 (Eigenstate)	特征向量 (Eigenvector)
本征值 (Eigenvalue)	特征值 (Eigenvalue)
右矢 (ket) \(\\|a \rangle\)	列向量 (Column Vector)
左矢 (bra) \(\langle a\\|\)	行向量 (Row Vector)
\(\langle a\\|b\rangle\)	\(a\) 和 \(b\) 向量的内积 (Inner Product)
\(\\|a\rangle\langle b\\|\)	\(a\) 和 \(b\) 的外积构成的投影矩阵
基态 (Ground State)	最小本征态 (Eigenstate with Lowest Eigenvalue)
算符 (Operator)	矩阵 (Matrix)
线性算符 (Linear Operator)	线性变换 (Linear Transformation)
幺正 (酉) 算符 (Unitary Operator)	正交矩阵 (Orthogonal Matrix)
厄米矩阵 (Hermitian Matrix)	自伴矩阵 (Self-adjoint Matrix)
线性叠加原理 (Principle of Superposition)	线性组合性质 (Linearity)
投影算符 (Projection Operator)	投影矩阵 (Projection Matrix)

幺正矩阵与厄米矩阵

正交矩阵 (实数): \(AA^T = I\)
幺正矩阵 (复数): \(UU^\dagger = I\) (其中 \(\dagger\) 是共轭转置)
- 在量子计算中至关重要，因其性质保证了量子态经过幺正算子后仍是一个有效的量子态。
厄米矩阵 (复数): \(H = H^\dagger\)
- 其性质保证了本征值是实数，本征向量是正交的，这确保了量子系统的物理量是可观测的。

量子比特的物理实现¶

叠加特性: 电子自旋叠加、能量态叠加等物理过程的抽象就是量子比特的叠加特性。
- 电子自旋向上和自旋向下存在叠加。
- 原子的基态和激发态也存在叠加。
- 经典微电子电路的CMOS开关的开闭承载了1比特的信息。

DiVincenzo 判据 (量子计算机实现条件)¶

具有可操控的量子比特，并具有可扩充性（可调控的二能级系统）。
能够将量子比特的状态初始化为简单基准状态（设置 \(|0\rangle\) 态或 \(|1\rangle\) 态）。
具有长相关退相干时间（确保充足的时间有效完成计算任务）。
具有一组“通用”量子门（确保能够满足所有的计算任务需求）。
能够测量特定量子比特（完成量子信息到经典信息的转换）。

量子态基本概念¶

量子叠加态 (Superposition): 量子比特 (Qubits) 可以同时代表1和0的多种可能性组合。研究人员使用精密激光或微波束操纵，使量子比特处于叠加态。
量子纠缠态 (Entanglement): 一对量子比特对的两个量子比特存在于单个量子状态。改变其中一个量子比特的状态时，另一个量子比特的状态会瞬间改变。

量子比特的叠加态¶

量子比特: 存在两个可能的状态 \(|0\rangle\) 和 \(|1\rangle\)。与经典比特不同，量子比特可以处于 \(|0\rangle\) 和 \(|1\rangle\) 以外的状态，是状态的线性组合，称为叠加态。
表示: \(|\psi\rangle = \alpha|0\rangle + \beta|1\rangle\)
- \(\alpha\) 和 \(\beta\) 是复数 (振幅)，描述量子比特的叠加状态。
- \(|0\rangle\) 和 \(|1\rangle\) 是基矢态，构成二维复向量空间的正交基。
归一化条件: \(|\alpha|^2 + |\beta|^2 = 1\)
- 量子比特的状态是二维复向量空间中的单位向量。
- 向量各分量为复数，欧几里得范数为1。

量子比特的基矢态¶

除了 \(|0\rangle\) 和 \(|1\rangle\)，任意两个单位正交基都可以作为量子态的基矢态。
常用正交基:
- \(|+\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\)
- \(|-\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)\)
任意量子态都可以表示为这组基的线性组合: \(|\psi\rangle = \alpha|+\rangle + \beta|-\rangle\)

量子比特的向量表示¶

\(|0\rangle\) 和 \(|1\rangle\) 向量形式: \(|0\rangle = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\), \(|1\rangle = \begin{bmatrix} 0 \\ 1 \end{bmatrix}\)
\(|+\rangle\) 和 \(|-\rangle\) 向量形式: \(|+\rangle = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ 1 \end{bmatrix}\), \(|-\rangle = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ -1 \end{bmatrix}\)
任意量子态 \(|\psi\rangle = \alpha|0\rangle + \beta|1\rangle\) 向量形式: \(|\psi\rangle = \begin{bmatrix} \alpha \\ \beta \end{bmatrix}\)

量子态矢内积¶

Bra-ket 表示法: \(| \psi \rangle\) 表示列向量，\(\langle \psi |\) 表示其共轭转置行向量 \(\begin{bmatrix} \alpha^* & \beta^* \end{bmatrix}\)。
内积: \(\langle \psi | \psi \rangle = \alpha^* \alpha + \beta^* \beta = 1\) (标量)
一般定义: \(\langle a|b \rangle = a_0^* b_0 + a_1^* b_1 + \dots + a_n^* b_n\)
正交: 两个向量的内积为0。
欧几里得范数: \(|||v\rangle|| = \sqrt{\langle v|v \rangle}\)

量子态的坍缩¶

当测量量子态时，会发生量子态的坍缩 (投影)。
对于 \(|\psi\rangle = \alpha|0\rangle + \beta|1\rangle\)，将以 \(|\alpha|^2\) 的概率得到 \(|0\rangle\) 态，以 \(|\beta|^2\) 的概率得到 \(|1\rangle\) 态。
归一化条件: \(|\alpha|^2 + |\beta|^2 = 1\)。

不可克隆原理 (Quantum No-Cloning Theorem)¶

核心思想: 不能创建一个完美的克隆 (拷贝) 任意未知的量子态。
数学表示: 不存在一个线性算符 \(U\)，可以将量子态 \(|\psi\rangle\) 映射到相应的复制态 \(|\psi\rangle|\psi\rangle\)。
意义: 无法通过制作副本对量子态进行重复测量。

量子比特的几何表示 (Bloch 球)¶

可视化: 单量子比特的量子态可以可视化在一个球面中，称为 Bloch 球。
表示: \(|\psi\rangle = \cos(\frac{\theta}{2})|0\rangle + e^{i\varphi} \sin(\frac{\theta}{2})|1\rangle\)
- \(\theta\) 和 \(\varphi\) 是球坐标下的分量，且量子态的欧几里得范数为1。
全局相位: 量子态乘以一个单位模长的复数，只会引入一个全局相位，不会带来任何可观测的效应。
- \(|\psi'\rangle = e^{i\xi}|\psi\rangle\) 与 \(|\psi\rangle\) 物理等价。
注意: Bloch 球只能可视化 单个量子比特 的状态。

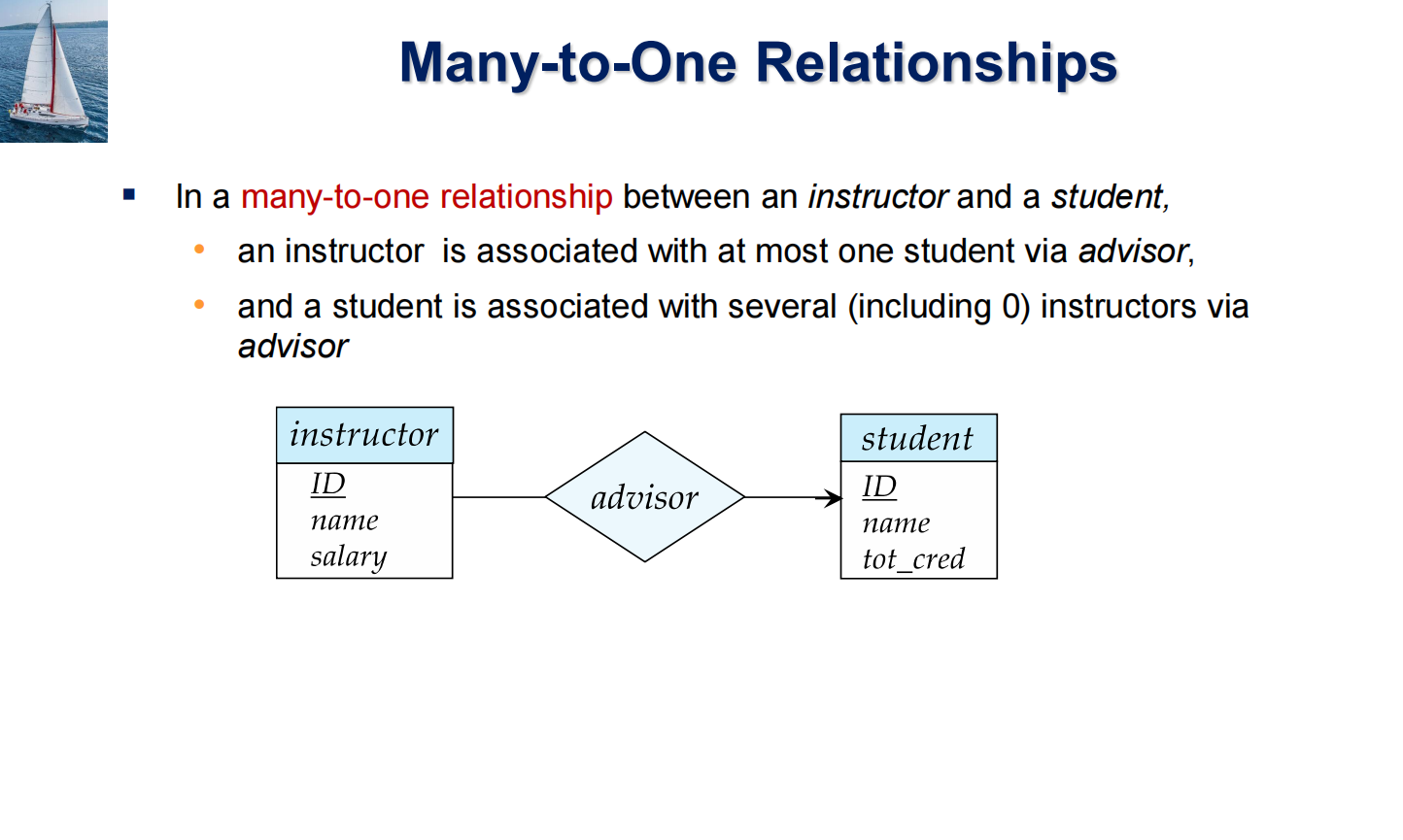
alt text

小结: 量子信息的无限与有限¶

无限: 一个量子比特的状态可以是Bloch球上的任意一点，复系数可以无限拓展，理论上一个量子比特的信息容量足以存储下一本书！
有限: 量子力学的基本假设限定了量子比特被测量后便会坍缩，单次测量只能获取一比特的信息。只有在测量了无数多个“完全相同”的量子比特后，才能确定 \(\alpha\) 和 \(\beta\)。
隐含信息: 在一个量子比特的状态里，大自然隐藏了大量的“隐含信息”，这些信息会随着量子比特数的增长而指数增长。

2. 多量子比特¶

多量子比特叠加态¶

两个量子比特: 有四种基本状态 \(|00\rangle, |01\rangle, |10\rangle, |11\rangle\)。
叠加态: 可以是这些基本态的叠加: \(|\psi\rangle = \alpha_{00}|00\rangle + \alpha_{01}|01\rangle + \alpha_{10}|10\rangle + \alpha_{11}|11\rangle\)
测量: 测量量子系统，以 \(|\alpha_x|^2\) 的概率得到 \(|x\rangle\) 态。
归一化: \(\sum_{x \in \{0,1\}^2} |\alpha_x|^2 = 1\)。
局部测量与坍缩: 测量其中低位量子比特得到0，则状态坍缩并归一化。
N个量子比特: \(2^N\) 种基本状态。

张量积 (Tensor Product / Kronecker Product)¶

定义: 用于组合向量空间的运算，将两个向量空间的向量合并成一个更大的向量空间。
表示: \(V \otimes W\)。结果是一个新的向量空间，其维度等于 \(V\) 和 \(W\) 的维度的乘积。
示例:
- 向量表示: \(\begin{bmatrix} \alpha \\ \beta \end{bmatrix} \otimes \begin{bmatrix} \gamma \\ \delta \end{bmatrix} = \begin{bmatrix} \alpha\gamma \\ \alpha\delta \\ \beta\gamma \\ \beta\delta \end{bmatrix}\)
- 作用: 获得多个量子态的复合量子态，提供多量子比特的数学表示方法。

判断是否纠缠¶

无关/可分态: 如果一个多量子比特系统可以分解为多个单量子比特的张量积。
- 例如: \(\frac{1}{2}(|00\rangle + |01\rangle - |10\rangle - |11\rangle) = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle) \otimes \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\)
- 这意味着第二个比特的状态与第一个比特无关。
不可分/纠缠态: 如果无法分解成多个单量子比特的张量积。
- 例如: \(\frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)\)
- 第一个比特测得0，第二个比特一定为0；第一个比特测得1，第二个比特一定为1。

复合系统与多比特门¶

编号与绘制: 态矢量中的每个量子比特按从左到右顺序编号，并在量子电路图中从上至下绘制。
多比特门: 若将两个单量子门视作一个整体，可以通过张量积的形式构成一个双量子门。

量子优势案例¶

量子计算机可以通过同时尝试所有可能的“钥匙”来一次性解决问题 (如开锁)，而经典计算机需要依次尝试。
这种优势源于量子叠加态和量子纠缠态的特性。

贝尔态 (Bell States)¶

定义: 双量子比特系统中重要的纠缠态。
四种贝尔态:
- \(|\phi^+\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)\)
- \(|\phi^-\rangle = \frac{1}{\sqrt{2}}(|00\rangle - |11\rangle)\)
- \(|\psi^+\rangle = \frac{1}{\sqrt{2}}(|01\rangle + |10\rangle)\)
- \(|\psi^-\rangle = \frac{1}{\sqrt{2}}(|01\rangle - |10\rangle)\)
贝尔基: 这四个贝尔态构成一个基底，任何双量子比特的量子态都可以表示为它们的线性组合。

3. 单量子门¶

引入: 量子非门 (Pauli-X 门)¶

经典X门 (NOT门): 翻转电平信号 (0态和1态交换)。
量子X门: 作用是线性的，实现 \(|0\rangle \rightarrow |1\rangle\) 的转变，互换复系数。
矩阵表示: \(X = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\)
结论: 单量子比特的量子门可以由 \(2 \times 2\) 的矩阵给出，其矩阵分量决定了量子门的行为。

Hadamard 门 (H 门)¶

基础量子门: 将 \(|0\rangle\) 和 \(|1\rangle\) 转变为叠加态。
矩阵表示: \(H = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}\)
作用:
- \(H|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) = |+\rangle\)
- \(H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle) = |-\rangle\)
几何意义: 将量子态从z基到x基的转变；或在Bloch球上先绕z轴转180度再绕y轴转90度；或围绕x-z轴中界线旋转180度。

Pauli 矩阵和 Pauli 门 (X, Y, Z)¶

Pauli-X 矩阵: \(\sigma_x = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\)
Pauli-Y 矩阵: \(\sigma_y = \begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}\)
Pauli-Z 矩阵: \(\sigma_z = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\)
作用:
- X门: 实现 \(|0\rangle \leftrightarrow |1\rangle\) 转变，相当于绕x轴旋转 \(\pi\) 角度。
- Y门、Z门: 分别让量子态绕y轴和z轴旋转 \(\pi\) 角度。

量子门与矩阵乘法¶

量子计算本质: 酉矩阵计算！
表示: \(V' = UV\) (输出态 = 演化矩阵 \(\cdot\) 输入态)
可逆性: \(V = U^{-1}V'\)
正则性: \(||U|| = 1\)
量子门的例子: Hadamard (H), Pauli-Y (Y), Pauli-Z (Z), CNOT。

厄米矩阵和酉矩阵 (重复，此处为总结)¶

量子门的矩阵限制: 只有酉矩阵才能用作表示一个量子门！
厄米矩阵 (\(A=A^\dagger\)): 其性质保证了本征值是实数，本征向量是正交的，这确保了量子系统的物理量是可观测的。
酉矩阵 (\(UU^\dagger=I\)): 其性质保证了作用在量子态上得到的结果仍然满足归一化条件 (合法量子态)；保持内积不变 (保持态矢量间的正交性质)。

相位旋转门 (P, S, T 门)¶

作用: 引入特定的相位因子，改变量子态的相对相位，但不改变其概率分布。
应用: 量子相位估计、量子傅里叶变换等。
与Pauli门区别: 不涉及量子比特的旋转操作，而是旋转相位。
常见门:
- P门: \(P = \begin{bmatrix} 1 & 0 \\ 0 & e^{i\varphi} \end{bmatrix}\) (将量子比特的相位进行旋转，\(\varphi\) 为输入参数)
- S门: \(S = \begin{bmatrix} 1 & 0 \\ 0 & i \end{bmatrix}\) (P门的特例，\(\varphi = \pi/2\))
- T门: \(T = \begin{bmatrix} 1 & 0 \\ 0 & e^{i\pi/4} \end{bmatrix}\) (P门的特例，\(\varphi = \pi/4\))

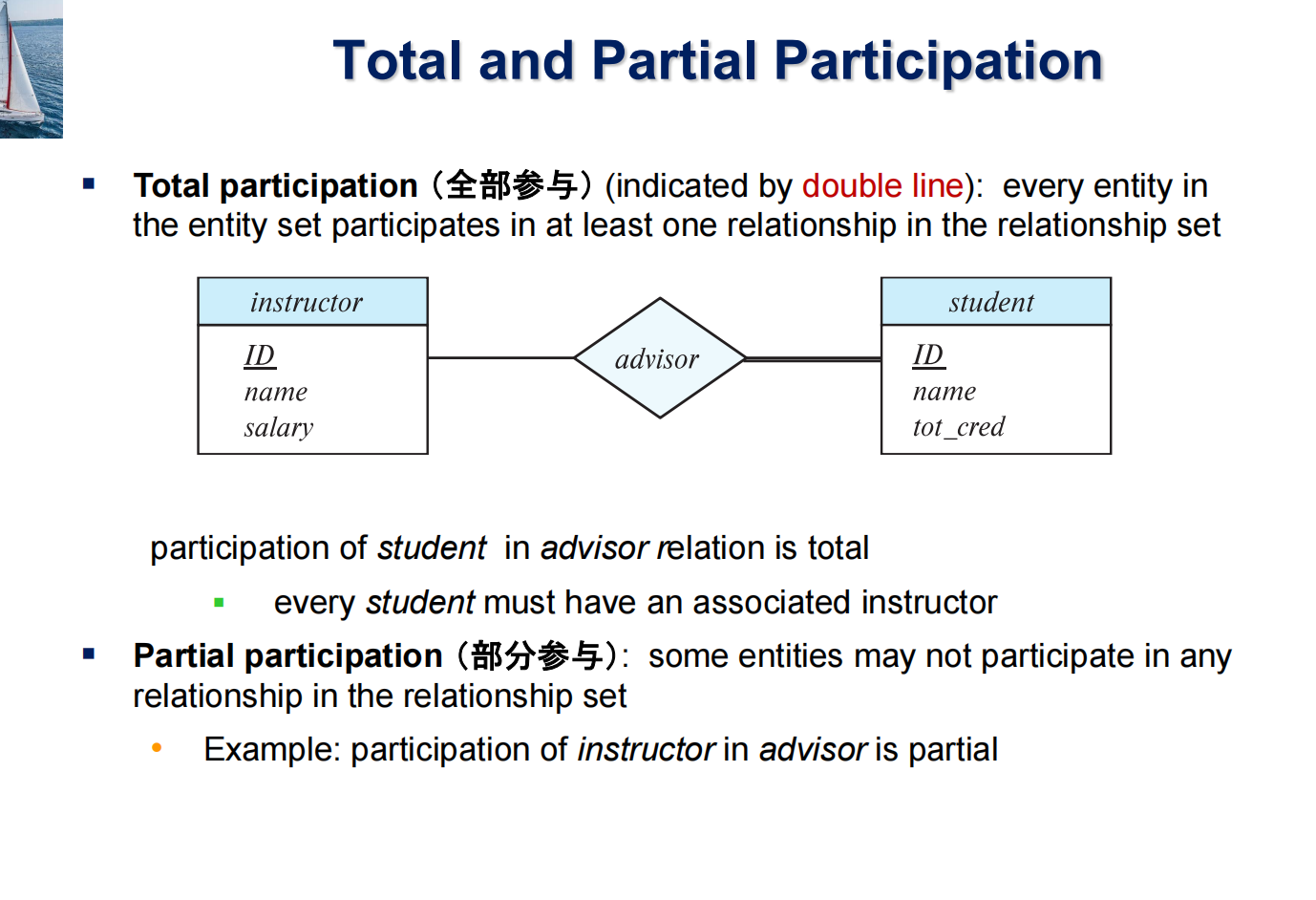
alt text

参数旋转门 (\(R_x(\theta), R_y(\theta), R_z(\theta)\))¶

基本门: 允许根据给定参数执行量子态的旋转操作。
常见门: 绕X轴、Y轴和Z轴的旋转门，\(\theta\) 是旋转角度。
- \(R_x(\theta) = \begin{bmatrix} \cos(\frac{\theta}{2}) & -i\sin(\frac{\theta}{2}) \\ -i\sin(\frac{\theta}{2}) & \cos(\frac{\theta}{2}) \end{bmatrix}\)
- \(R_y(\theta) = \begin{bmatrix} \cos(\frac{\theta}{2}) & -\sin(\frac{\theta}{2}) \\ \sin(\frac{\theta}{2}) & \cos(\frac{\theta}{2}) \end{bmatrix}\)
- \(R_z(\theta) = \begin{bmatrix} e^{-i\theta/2} & 0 \\ 0 & e^{i\theta/2} \end{bmatrix}\)
应用: 量子电路设计、量子机器学习 (如量子神经网络、变分量子算法)。

单量子比特操作分解¶

问题: 任何2x2的酉矩阵都可以表示一个量子门，但酉矩阵有无穷多个，需要制造这么多门吗？
答案: 不需要。任意一个2x2的酉矩阵都可以分解为: \(U = e^{i\alpha} \begin{bmatrix} e^{-i\beta/2} & 0 \\ 0 & e^{i\beta/2} \end{bmatrix} \begin{bmatrix} \cos(\frac{\gamma}{2}) & -\sin(\frac{\gamma}{2}) \\ \sin(\frac{\gamma}{2}) & \cos(\frac{\gamma}{2}) \end{bmatrix} \begin{bmatrix} e^{-i\delta/2} & 0 \\ 0 & e^{i\delta/2} \end{bmatrix}\)
- 这个分解可以对任意单比特操作进行精确描述，这意味着只需要有限数量的基本门 (如旋转门和Pauli门) 即可实现任意单比特操作。

4. 多量子门¶

从XOR门到CNOT门¶

经典XOR门: “受控非门”；输入A是“控制端”，A为1时，XOR对B施加非门；A为0时，不施加非门。
量子CNOT门 (Controlled-NOT Gate): 一种受控门。
- 控制比特: 其状态决定目标比特是否翻转。
- 目标比特: 当控制比特为 \(|1\rangle\) 时翻转，为 \(|0\rangle\) 时保持不变。
矩阵表示: \(CNOT = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix}\) (控制比特为q0，目标比特为q1)
真值表 (非叠加态): | Input (c t) | Output (c t) | | :---------- | :----------- | | 0 0 | 0 0 | | 0 1 | 0 1 | | 1 0 | 1 1 | | 1 1 | 1 0 |

基于CNOT门制备贝尔态¶

主要作用: 制备纠缠态。
制备 \(|\phi^+\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)\) 的电路:
1. 初始化 q0 和 q1 为 \(|00\rangle\)。
2. 对 q0 施加 Hadamard 门 (\(H\))，使 q0 处于叠加态。
3. 对 q0 和 q1 施加 CNOT 门，q0 为控制比特，q1 为目标比特。
结果: \(|00\rangle \xrightarrow{H \text{ on } q0} \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)|0\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |10\rangle)\) \(\xrightarrow{CNOT} \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)\)

量子隐形传态 (Quantum Teleportation)¶

目的: 将一个未知量子态从Alice传输给Bob。
核心机制:
1. Alice和Bob共享一个纠缠态 (如贝尔态)。
2. Alice拥有待传输的未知量子态 \(|\psi\rangle\) 和纠缠对中的一个比特。
3. Alice对自己的两个比特 (未知态和纠缠态中的一个) 进行操作 (CNOT，Hadamard) 和测量。
4. Alice通过 经典信道 将测量结果 (2比特经典信息) 发送给Bob。
5. Bob根据收到的经典信息对自己的纠缠态比特进行操作 (X, Z 门)，恢复出Alice的未知量子态。
关键点:
- 不可克隆原理: Alice无法直接复制未知态。
- 经典通信: 传输过程中需要经典信道，因此量子隐形传态不能突破光速限制。
- 不是拷贝: 最终实现了量子比特的传输，而不是拷贝，因为Alice端的原始量子态在测量后坍缩。

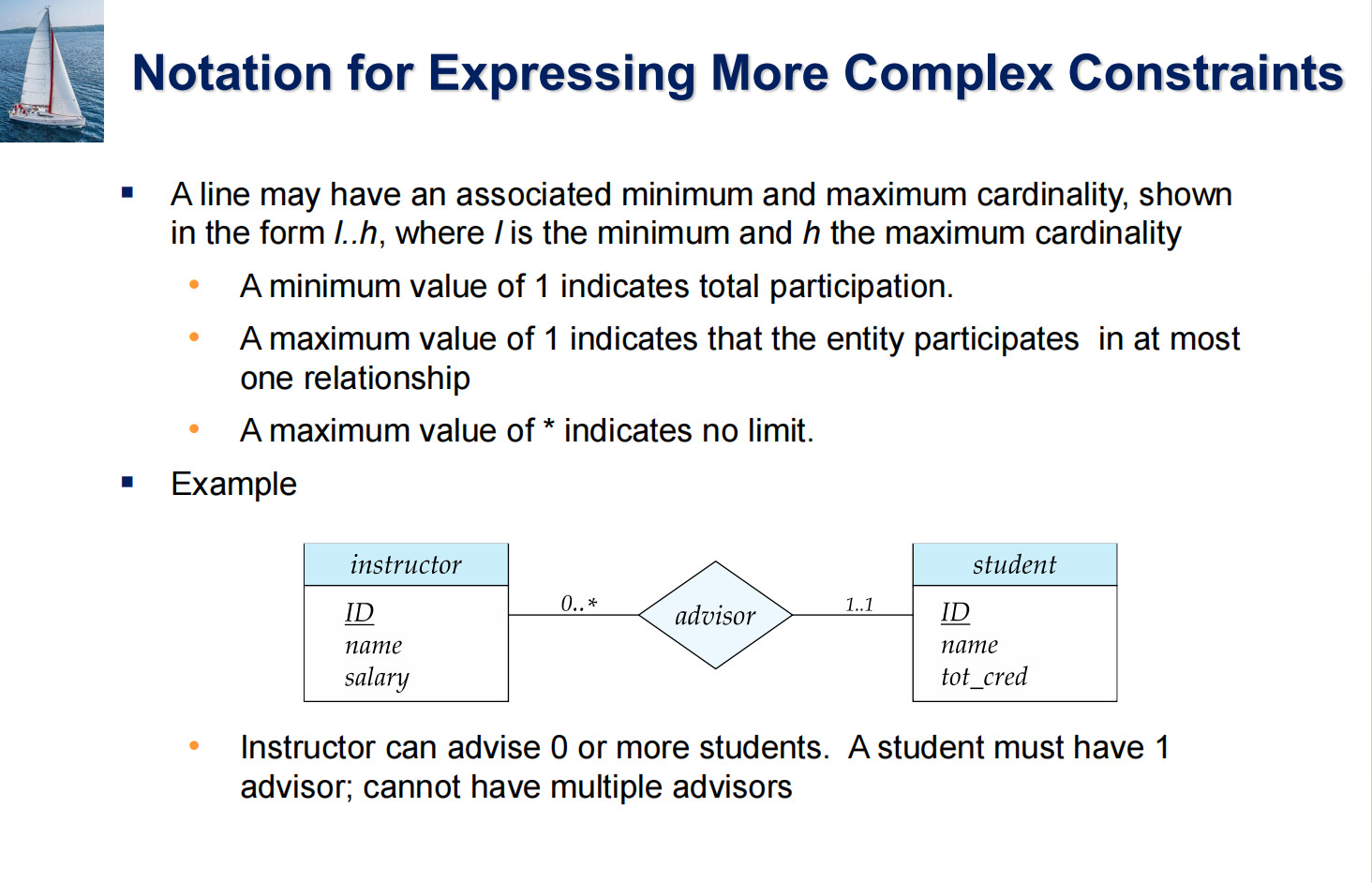
alt text

SWAP门及CSWAP门¶

SWAP门: 交换两个量子比特的状态。
矩阵表示: \(SWAP = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\)
作用: 生成和操作纠缠态，通过交换可以创建新的纠缠态。
CSWAP门 (Controlled-SWAP / Fredkin门): 给SWAP门添加一个控制比特。当控制比特为 \(|1\rangle\) 时，执行SWAP操作；否则不变。

SWAP操作在硬件上的应用¶

问题: 现阶段量子计算机中，逻辑上相邻的量子比特在物理硬件上可能不相邻。
解决方案: SWAP操作可以将物理比特“交换”位置，从而实现对不相邻逻辑比特的多比特门操作。
重要性: 成为量子线路编译及优化中常用的技术。

Toffoli门 (CCNOT / CCX 门)¶

三量子比特门: 在经典计算中执行AND逻辑操作。
操作: 如果前两个量子比特 (控制比特) 都处于 \(|1\rangle\) 态，则对第三个量子比特 (目标比特) 执行非门操作；否则目标比特保持不变。
矩阵表示: \(8 \times 8\) 矩阵，只在最后两行倒数第二列和倒数第一列对调。
广义形式: 可以有更多控制比特 (CCCNOT, CCCCNOT 等)。

alt text

量子计算的并行性¶

基本特征: 量子计算机可以同时计算 \(f(x)\) 在多个 \(x\) 取值下的函数值。
映射: \(|x, y\rangle \rightarrow |x, y \oplus f(x)\rangle\) (其中 \(\oplus\) 是模2加运算)。
原理: 利用叠加态，在单个电路中同时计算多个函数值。
实现: 对输入 \(x\) 的每个比特施加Hadamard门，将其置于平衡叠加态 \(\frac{1}{\sqrt{2^n}}\sum_x |x\rangle\)。
输出: \(\frac{1}{\sqrt{2^n}}\sum_x |x\rangle |f(x)\rangle\)

从并行性到Deutsch算法¶

问题: 经典计算中，要确定一个未知函数 \(f: \{0,1\} \rightarrow \{0,1\}\) 是常数函数 (\(f(x)=0\) 或 \(f(x)=1\)) 还是平衡函数 (\(f(0) \neq f(1)\))，至少需要2次查询。量子计算机能否更高效？
Deutsch算法:
1. 初始化: 输入比特 \(|0\rangle\) 和 \(|1\rangle\)，第二个比特通过Hadamard门得到 \(|-\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)\)。
2. Oracle操作: 将 \(U_f\) 作用在 \(|x\rangle |-\rangle\) 上，利用性质 \(|x\rangle |y \oplus f(x)\rangle = |x\rangle (-1)^{f(x)} |y\rangle\) 得到 \(|x\rangle (-1)^{f(x)} |-\rangle\)。
3. Hadamard门: 对第一个比特再施加Hadamard门。
4. 测量: 测量第一个比特。
结果:
- 如果测量结果是 \(|0\rangle\)，则 \(f\) 是常数函数。
- 如果测量结果是 \(|1\rangle\)，则 \(f\) 是平衡函数。
优势: 只需 一次计算、一次测量 即可确定函数 \(f\) 的全局性质，比经典计算 (至少2次) 更快。
本质: 通过精心选择函数以及变换，以优于经典计算的速度获取函数的全局信息。

alt text

Oracle¶

概念: 在量子计算中，Oracle 代表一个功能，其行为已知 (输入输出关系)，但内部实现细节可能未知，被视为“黑盒”。
作用: 输入数据，输出 1 (yes) 或 0 (no)。
要点:
- 尽可能快速高效。
- 调用Oracle的次数尽可能少，减少算法复杂度。
表示:
- 经典: \(f: \{0,1\}^n \rightarrow \{0,1\}\)
- 量子: \(f(|\psi\rangle) = |1\rangle\) (如 \(|\psi\rangle = |1000\rangle\)) 或 \(|0\rangle\) (其它)。

Oracle线路设计与简化¶

设计: 包含待判断的函数 \(f(x)\)，传入量子比特，输出可区分常量或平衡函数的量子比特。
- \(U_f: |x\rangle |y\rangle \rightarrow |x\rangle |y \oplus f(x)\rangle\)
- 通常 InputA 固化为 \(|0\rangle\) 作为辅助输入，OutputA 是真实操作结果。
四种基本函数对应的线路: \(f(x)=0\), \(f(x)=1\), \(f(x)=x\), \(f(x)=\neg x\)。
线路简化规则:
1. \(H \cdot H = I\) (Hadamard门自身逆)
2. \(H \cdot X \cdot H = Z\)
3. CNOT门的等效变换。

alt text

量子电路部署流程¶

电路层编译:
1. 量子程序: 编写量子算法。
2. 量子电路 (逻辑电路): 硬件无关优化。
3. 量子电路 (物理电路): 硬件相关优化，将逻辑门映射到物理比特和它们的连接。
4. 板卡指令: 将物理电路转换为量子硬件可执行的指令集。
波形层编译:
1. 脉冲: 将板卡指令转换为具体的微波脉冲序列。
2. 量子真机: 执行脉冲序列。
波形生成:
- 每种基础门都有对应的波形。
- 量子门转换为量子芯片可识别的波形是波形层编译的一部分。
- 波形生成过程中量子门的时序不能改变，门的时序同时也是波形的时序。
- 两比特量子门每个比特有两段波形，单门波形一般只有一段。